An equation expresses the equality of two mathematical expressions.

An equation always contains an equal sign.

A solution of an equation is a number that, when substituted for the variable, results in a true equation.

To solve an equation is to find all solutions for the equation.

Equivalent equations are equations that have exactly the same solutions. When solving equations, we usually try to find equivalent equations until we get to

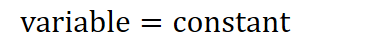
A few things we can do that result in equivalent equations:

Add numbers to both sides of an equation
Multiply both sides by a nonzero number
Replace things that are equal with each other

If you need more practice with these, here is a worksheet on solving multi-step linear equations.

Contradictions, Conditional Equations and Identities

An equation that has no solutions is called a contradiction.

An equation that is true for some values of the variable, but not true for others is called a conditional equation.

An identity is an equation that is true for all values of the variable for which all terms of the equation are defined. It has an infinite number of solutions.

Absolute Value Equations

The absolute value of a number is the “non-negative” version of that number. The absolute value of is written $|x|$

So the absolute value of -7 is 7 and the absolute value of 9 is 9. The absolute value of 0 is 0.

Formally, |x| = x if $x\geq 0$ and |x|=-x (which is nonnegative) if $x<0$

Here is a worksheet for extra problems on absolute value equations.